前々回（第139回）で、1日の大当り回数分布の大きなグラフを掲載した。5万日のシミュレート結果を、大当り0回から71回まで1回刻みに仕分けし、分布グラフに表したものだ。

コレがそのグラフ。

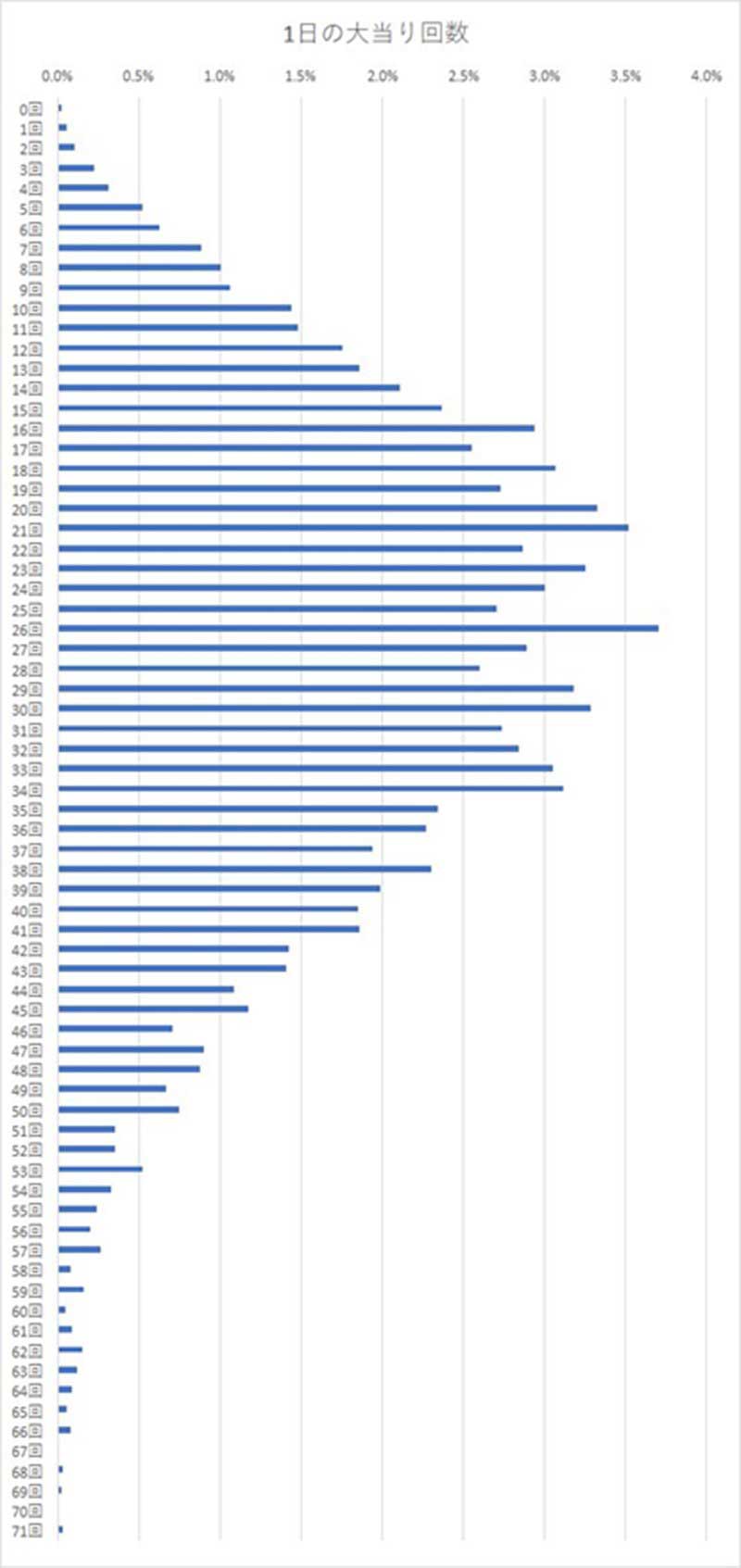
このグラフを90°回転させると、大ざっぱに言えば富士山のような形状になっている。

しかし細部を見ると実は凹凸だ。最も棒が長い（山が高い）のは大当り26回の部分だが、その隣の25回と27回は周囲と比べてかなり凹んでいる。本来ならば頂点からな徐々に棒が短くなっていくキレイな山型曲線を描くはずだが、このグラフでは結構ガタガタした山型になっている。

この原因として最初に思いつくのはサンプル数の少なさだ。シミュレート日数が少なければ結果にバラツキが出やすくなる。

それならばシミュレート日数を増やせばいいのか？

いや、実はこの場合、シミュレート日数を10万日、20万日と増やしたところでグラフの凸凹は滑らかにならない。では何が原因なのか？

本当の原因は「パソコン乱数」にある。

パソコンで生成した乱数は一見規則性がないように見えても長期的には一定のパターンができてしまう。そのような乱数の不完全さが現れてしまったのが上記の凸凹グラフだったのだ。

一応断っておくが、不完全な乱数でもちゃんと確率は収束するし、勝率、平均収支、平均投資額を出すには全く問題がない。大当り回数分布に関しても従来のように5回刻みで出すのならば問題ない。簡単に言ってしまえば、普段パチマガスロマガFREEやMobileに載せているようなシミュレート数値ならば信頼して大丈夫ということになる。

しかし分類条件を細分化するほど問題が出てきてしまう。その不完全さを補う方法もないわけではないが、決して完璧にはならない。

ところで、本連載ではパチンコで勝つために役立つ事しか書かないと常々公言している。ならば今回の解説が勝つために何の役に立つのか？

それは、パチンコ機で生成される乱数はそのようなパターンができてしまう心配は全くないということだ。釘や玉といった流動的なものから乱数を作っているので特定のパターンが出現しないのだ。

パチンコの大当り抽選に使用されているコンピュータはそれほど高性能なものとは言えないが、こと乱数の生成に関しては私のPCよりはるかに完璧である。余計なことを考えずに確率論だけを信じて臨めばいい。